【Applications of ultradiscretization to nonlinear phenomena】
key words:nonlinear dynamics, ultradiscretization, max-plus algebra, cellular automaton, stochastic process
-
Ultradiscrete dynamical system(max-plus dynamical system)
Ultradiscretization is applied to dynamical models with bifurcation phenomena, and the dynamical properties of the derived ultradiscrete equations (max-plus equations) are studied from the viewpoint of non-linear dynamical systems. Also the construction of ultradiscrete dynamical systems is tackled by identifying the ultradiscrete equations with of piecewise linear discrete dynamical systems. 【References】 : Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 65 082705(2024). Shousuke Ohmori and Yoshihiro Yamazaki, AIP Conference Proceedings, in press. Shousuke Ohmori and Yoshihiro Yamazaki, JSIAM Letters, 14 127 (2022). Yoshihiro Yamazaki and Shousuke Ohmori, J. Phys. Soc. Jpn., 90 103001 (2021). Shousuke Ohmori and Yoshihiro Yamazaki, 京都大学数理解析研究所(RIMS)講究録, 2223 44 (2021). 大森祥輔, 山崎義弘, 津田塾大学, 数学・計算機科学研究所報, 42 103 (2021) . Shousuke Ohmori and Yoshihiro Yamazaki, unpublished, arXiv:2107.02435v1 [nlin.CD]. Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 61 122702 (2020).
-
Dynamics of Tropical discretized equations
The tropical discretization (Nonstandard finite difference scheme) is the discretization, under which continuous models can be ultradiscretized to ultradiscrete equations. By focusing on the dynamics of the difference equations derived from continuous systems by the tropical discretization, the relationship between continuous and ultra-discrete dynamical systems is studied. 【References】 : Yoshihiro Yamazaki and Shousuke Ohmori, JSIAMLetters, 16 85 (2024). Shousuke Ohmori and Yoshihiro Yamazaki, RIMS Kokyuroku Bessatsu, 94 55 (2023). Yoshihiro Yamazaki and Shousuke Ohmori, PTEP, 081A01 (2023). Shousuke Ohmori and Yoshihiro Yamazaki, JSIAM Letters, 15 73 (2023). Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 64 042704 (2023).
-
Ultradiscretization for pattern formation
Applications of the ultradiscretization to pattern formation phenomena, such as the FitzHugh-Nagumo reaction-diffusion model and the differential-difference equation reproducing patterns from adhesive tape peeling experiments, are studied. In particular, the CA patterns caused by ultradiscrete equations are focused on. 【References】 : Shousuke Ohmori and Yoshihiro Yamazaki, J. Phys. Soc. Jpn., 88 105001 (2019) . Yoshihiro Yamazaki and Shousuke Ohmori, Nanosystems: Phys., Chem., Math., 8 38 (2017). Shousuke Ohmori and Yoshihiro Yamazaki, J. Phys. Soc. Jpn., 85 014003 (2016). Shousuke Ohmori and Yoshihiro Yamazaki, PTEP, 083A01 (2014).
Gallery
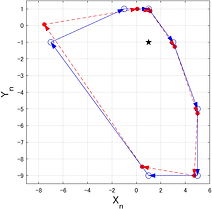
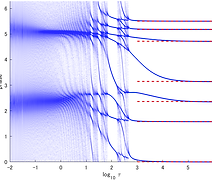
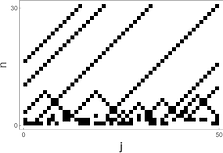
【General Topological approach to geometric patterns】
key words:general topology, disordered systems, continuum theory, 0-dim, fractal
Gallery
-
Topological representation of patterns by Cantor cube model
Characterization of the gemoetric patterns found in disordered matters are studied based on the general topology. In particular, Continuum theory that is one of the field of general topology has the powerful tool to describe geometric patterns. For instance, the dendrite structures found in metal solidification processes can be described in this context as 'a Peano-continua that does not contain a simple closed curve'. Such description of geometric patterns based on the concept and theorems in Continuum theory and uniformly representation of patterns by a Cantor cube are studied. 【References】 : Shousuke Ohmori, Yoshihiro Yamazaki, Tomoyuki Yamamoto, and Akihiko Kitada, AIP Conference Proceedings, in press. 大森祥輔, 九州大学マス・フォア・インダストリ研究所(IMI),材料科学における幾何学と代数III MIレクチャーノート, 89 128 (2022) . Shousuke Ohmori, 京都大学数理解析研究所(RIMS)講究録, 2209 75 (2021). Shousuke Ohmori,Yoshihiro Yamazaki, Tomoyuki Yamamoto, and Akihiko Kitada, Phys. Scrip., 94 105213 (2019). 大森祥輔, 京都大学数理解析研究所(RIMS)講究録, 2064 53 (2018) . Akihiko Kitada, Shousuke Ohmori, and Tomoyuki Yamamoto, J. Phys. Soc. Jpn., 85 045001 (2016).

-
Fractals and 0-dimensional space
Focusing on the concepts of "0-dimensional" and "decomposition space" of a topological space, topological treatment of hierarchic structure of fractals are studied. Also the mathematical condition of occurrence fo the hierarchic structure and its topological classification are discussed. 【References】 : Akihiko Kitada, Shousuke Ohmori, Yoshihiro Yamazaki, and Tomoyuki Yamamoto, AIP Conference Proceedings, in press. Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 11 (2014). Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 5 (2014). Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 1 (2014). Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 1 1 (2013).

【Rigged Hilbert space and its application to quantum physics】
key words:rigged Hilbert space, bra-ket formalism, nonHermite operator, spectral decomposition,
topological vector space
-
Bra-ket formalism of non-Hermite quantum system based on RHS
The construction of RHS applicable to non-Hermitian quantum systems such that the Hamiltonian has a symmetric structure, e.g., PT-symmetric, and spectral decompositions for operators (observables) on it are studied. In particular, the rigorous treatment of bra-ket forms and the expansion of continuous spectra onto topological linear spaces is interesting. 【References】 : Shousuke Ohmori, 京都大学数理解析研究所(RIMS)講究録, 1 2314( 2025). Shousuke Ohmori, J. Math. Phys., 65 123502 (2024). Shousuke Ohmori and Junichi Takahashi, J. Math. Phys., 63 123503 (2022).