【非線形現象・パターン形成現象と超離散化】
『キーワード』:非線形動力学、超離散化、差分化、max-plus代数、セルオートマトン、確率過程
-
分岐現象に対する超離散化:超離散力学系(max-plus力学系)の体系化
超離散化法を力学系モデルへ適用し、導出される超離散方程式(max-plus方程式)の動力学的性質を非線形動力学の観点から研究しています。特に固定点の安定性や分岐現象を有するような力学系の構造が、超離散力学系においても保持されるのか着目しています。また、超離散方程式を区分線形離散力学系として捉えて体系化・実社会への応用を目指しています。 References : Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 65 082705(2024). Shousuke Ohmori and Yoshihiro Yamazaki, AIP Conference Proceedings, in press. Shousuke Ohmori and Yoshihiro Yamazaki, JSIAM Letters, 14 127 (2022) Yoshihiro Yamazaki and Shousuke Ohmori, J. Phys. Soc. Jpn., 90 103001 (2021) Shousuke Ohmori and Yoshihiro Yamazaki, 京都大学数理解析研究所(RIMS)講究録, 2223 44 (2021) 大森祥輔, 山崎義弘, 津田塾大学, 数学・計算機科学研究所報, 42 103 (2021) Shousuke Ohmori and Yoshihiro Yamazaki, unpublished, arXiv:2107.02435v1 [nlin.CD] Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 61 122702 (2020)
-
正値差分化の動力学:連続系から超離散系への動力学的遷移
Gallery
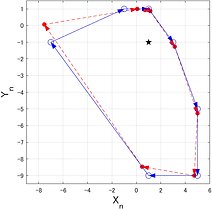
連続力学系から超離散力学系を導出する際、連続系は正値差分化と呼ばれる差分化によって変換され、その後超離散化されます。正値差分化(トロピカル差分化)によって得られる差分方程式の動力学に着目し、連続力学系と正値差分化による離散力学系、超離散力学系の力学的関係性を研究しています。 References : Yoshihiro Yamazaki, Shousuke Ohmori, JSIAMLetters, 16 85 (2024). Shousuke Ohmori and Yoshihiro Yamazaki, RIMS Kokyuroku Bessatsu, 94 55 (2023). Yoshihiro Yamazaki and Shousuke Ohmori, PTEP, 081A01 (2023) Shousuke Ohmori and Yoshihiro Yamazaki, JSIAM Letters, 15 73 (2023) Shousuke Ohmori and Yoshihiro Yamazaki, J. Math. Phys., 64 042704 (2023)
-
パターン形成現象と超離散化
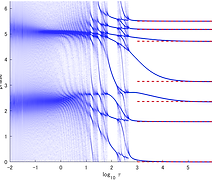
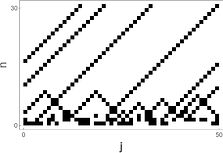
パターン形成現象に対する超離散化法の応用として、FitzHugh-Nagumo型反応拡散モデルや非対称局所的相互作用及び大域的相互作用を有する双安定素子の従う微差分方程式(粘着テープ剥離実験のパターンを再現)を対象に研究しています。 特に、得られる確率超離散方程式のセルオートマトンパターンに興味を持っています。 References : Shousuke Ohmori and Yoshihiro Yamazaki, J. Phys. Soc. Jpn., 88 105001 (2019) Yoshihiro Yamazaki and Shousuke Ohmori, Nanosystems: Phys., Chem., Math., 8 38 (2017) Shousuke Ohmori and Yoshihiro Yamazaki, J. Phys. Soc. Jpn., 85 014003 (2016) Shousuke Ohmori and Yoshihiro Yamazaki, PTEP, 083A01 (2014)
【一般位相空間論による物質の幾何学的パターンの表現】
『キーワード』:一般位相空間論、物質パターン、不規則系、連続体理論、0-dim(ゼロ次元)、フラクタル
-
Cantor cubeによる幾何学的パターンの位相表現
最も基本的なトポロジーである一般位相空間論(ジェネラルトポロジー)で用いられる定理や概念に基づいて、物質の幾何学的パターンの特徴づけを行っています。例えば、金属凝固過程などで出現するデンドライト構造は一般位相空間の言葉では「単純閉曲線を含まないPeano連続体」として記述できることが知られています。このような一般位相空間における連続体理論に現れる概念に基づいた物質の幾何学的パターンの特徴づけ、及びCantor cubeなる位相空間による幾何学的パターンの統一的な表現について研究しています。 References : Shousuke Ohmori, Yoshihiro Yamazaki, Tomoyuki Yamamoto, and Akihiko Kitada, AIP Conference Proceedings, in press. 大森祥輔, 九州大学マス・フォア・インダストリ研究所(IMI),材料科学における幾何学と代数III MIレクチャーノート, 89 128 (2022) Shousuke Ohmori, 京都大学数理解析研究所(RIMS)講究録, 2209 75 (2021) Shousuke Ohmori,Yoshihiro Yamazaki, Tomoyuki Yamamoto, and Akihiko Kitada, Phys. Scrip., 94 105213 (2019) 大森祥輔, 京都大学数理解析研究所(RIMS)講究録, 2064 53 (2018) Akihiko Kitada, Shousuke Ohmori, and Tomoyuki Yamamoto, J. Phys. Soc. Jpn., 85 045001 (2016)
-
フラクタルと位相的ゼロ次元空間との関係
一般位相空間論の次元論において定義される0-dim(ゼロ次元)空間や連続体理論を用いて、フラクタル構造の数学的側面を研究しています。特に、自己相似階層構造の位相空間論的表現や階層構造を生じるための数学的条件、分類を行っています。 References : Akihiko Kitada, Shousuke Ohmori, Yoshihiro Yamazaki, and Tomoyuki Yamamoto, AIP Conference Proceedings, in press. Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 11 (2014) Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 5 (2014) Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 2 1 (2014) Akihiko Kitada, Tomoyuki Yamamoto, Shousuke Ohmori, 早稲田大学凝縮系物質科学研究所紀要, Condensed-Matter Science Reports, 1 1 (2013)
Gallery


【Rigged Hilbert 空間と量子力学の数学的基礎付け】
『キーワード』:Rigged Hilbert 空間、bra-ket形式、nonHermite作用素、スペクトル分解、位相線形空間論
-
非エルミート量子系に対するRHSを用いた数学的定式化
Rigged Hilbert 空間(RHS) は、I. M. Gelfand によりHilbert 空間と超関数とを結びつけるために考案された位相線形空間の組で、量子力学などにみられるDirac のbra-ket 形式を数学的に定式化できることが知られています。このRHS に基づいたnonHermiter量子系などの現代量子論の数学的基礎付けに興味があります。特に、RHSがHilbert空間より広い空間であることに着目して、bra-ket形式の厳密な取り扱いや連続スペクトルの位相線形空間上の展開(nonHermite作用素のスペクトル分解)を研究しています。 References : Shousuke Ohmori and Junichi Takahashi, arXiv:2403.0023. Shousuke Ohmori, 京都大学数理解析研究所(RIMS)講究録, 1 2314( 2025). Shousuke Ohmori, J. Math. Phys., 65 123502 (2024). Shousuke Ohmori and Junichi Takahashi, J. Math. Phys., 63 123503 (2022)